クォータニオンから回転行列への変換を、数式と手計算で丁寧に導く【中編】
はじめに
「クォータニオンって難しそうだけど、仕組みを理解して自分で実装したい」
そんな方に向けて、回転行列⇔クォータニオンの仕組みを3部構成で丁寧に解説しています。
この記事は中編にあたり、クォータニオン→回転行列の変換式を手計算で導いていきます。
前編では、クォータニオンや回転行列、traceなどの変換の理解に必要な「土台となる基礎知識」を紹介しています。
まだ読んでいない方は、先にそちらから読んで頂くのがオススメです。
「最終的に目指すのは回転行列→クォータニオンの変換なのに、なぜ逆の変換からはじめるの?」と思うかもしれませんが、先にクォータニオンから回転行列を得る流れを理解しておくことで、後編の導出が驚くほど分かりやすくなります。
まずは「クォータニオンがどのように回転行列に変換されるのか?」を一緒に確認していきましょう。
本記事について(3部構成)
この記事は「回転行列→クォータニオン変換の式を自力で導出する」ことを最終目標とした、3部構成の中編です。
「導出なんて難しそう」と思うかも知れませんが、基礎知識さえ理解すれば、誰でもたどり着けるように工夫しています。
途中式を省略することなく丁寧に解説しているので、興味のあるところから読み進めてみてください。
この記事で解説する流れ
最終的には回転行列→クォータニオンの変換を目指していますが、その逆の「クォータニオン→回転行列」を求める方法を先に説明します。
なぜ逆のことを先に行なうの?と不思議に思うかもしれませんが、これには理由があります。
クォータニオンは、ある物体を回転させるために使います。
まず最初にクォータニオンを使ってベクトルを回転させ、その結果として得られる回転行列を導きます。
この回転行列を理解することで、「クォータニオン→回転行列」の仕組みがわかり、その後に逆の操作である「回転行列→クォータニオン」を求めることができます。
なにより、逆の仕組みを理解していると、後々出てくる数式の意味が理解しやすいです。
回りくどいですが、まずは、「クォータニオン→回転行列」を理解していきましょう!
クォータニオンから回転行列を求める
1. ベクトルをクォータニオンに変換する
クォータニオンは「ある物体を回転させるため」に使います。
ここでは、ベクトル $\overline{v} = \begin{pmatrix} v_x \ v_y \ v_z \end{pmatrix}$ を回転させるためにクォータニオンを使っていきましょう。
しかし、このままの形ではクォータニオンとして表現できません。
まずは、ベクトル $\overline{v} = \begin{pmatrix} v_x \ v_y \ v_z \end{pmatrix}$ をクォータニオンに変換します。
前回の記事で、クォータニオンは「スカラー部(実部)」と「ベクトル部(虚部)」から成ることを説明しました。
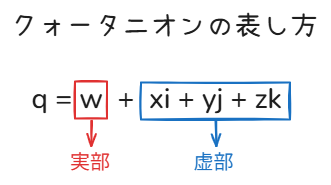
ここでベクトル $\overline{v} = \begin{pmatrix} v_x \ v_y \ v_z \end{pmatrix}$ をクォータニオンに変換するには、スカラー部を0にして、ベクトル部をそのまま使います。
結果として、次のような純クォータニオンになります。
$$v = 0 + v_xi + v_yj + v_zk
$$
これでベクトルがクォータニオンの形になっているから終わりじゃないの?と思うかもしれません。
実はこの形は一見クォータニオンになっているように見えますが、形だけなんです!
位置の情報をクォータニオンの形にしただけで、回転の情報はまだ含まれていません。
思い出してください。
クォータニオンは回転の情報などを $w, x, y, z$ と虚数単位を使って表していましたよね?
でも今の形はw成分がなくて、ただベクトルをクォータニオンの形に合わせただけです。
つまりここから、回転の情報を加えたベクトルの形(言い換えるならば、回転の情報を加えた純クォータニオン)にする必要があります。
まとめるとこんな感じです。
・今の状態はベクトルを純クォータニオンの形にしただけで、回転の情報を持っていない
・ここから回転の情報を持ったクォータニオンの形に変化させる
・最終的なゴールは回転の情報を持った純クォータニオン
では、次に回転情報を持たせるための計算を紹介します。
2. 回転後のベクトル $v'$ を求める
クォータニオンを使ってベクトルを回転させるためには、次の式を使います。
$$v' = q \cdot v \cdot \overline q
$$
ここで、
$$\begin{align}
&q: 単位クォータニオン \\
&v: 回転させたいベクトル \\
&\overline q: 共役クォータニオン
\end{align}
$$
を表しています。
なんでこの掛け算を行なうのか?という疑問は、実際の計算過程を追って説明していきます。
2-1. 単位クォータニオンをかける
まずは、単位クォータニオン $q$ を回転させたいベクトル $v$ にかけます。
$$v' = q \cdot v
$$
$q$ と $v$ は以下の通りです。
$$\begin{align}
&q = w + xi + yj + zk \\
&v = 0 + v_xi + v_yj + v_zk
\end{align}
$$
回転させたいベクトル $v$ は、クォータニオンの形にしただけで、ここに回転の情報は含まれていません。
単位クォータニオンをかけることで、「どんな回転をするのか」という情報が含まれます。
では実際に計算をしていきます。
ここから先はクォータニオンの積のルールに従って計算していきます。
具体的には、以下の規則です。
$$\begin{align}
&i^2 = j^2 = k^2 = -1 \\
&ijk = -1 \\
&ij = -ji = k \qquad jk = -kj = i \qquad ki = -ik = j
\end{align}
$$
この規則を元に $q \cdot v$ のそれぞれの項を地道に掛け合わせていきます。
なおこれ以降の式では、それぞれの成分を次のように色分けして表示します。
・$\textcolor{skyblue}{w}$成分→$\textcolor{skyblue}{青}$
・$\textcolor{pink}{x}$成分→$\textcolor{pink}{ピンク}$
・$\textcolor{yellowgreen}{y}$成分→$\textcolor{yellowgreen}{緑}$
・$\textcolor{orange}{z}$成分→$\textcolor{orange}{オレンジ}$
$$\begin{align}
q \cdot v &= (\textcolor{skyblue}{w}+\textcolor{pink}{xi}+\textcolor{yellowgreen}{yj}+\textcolor{orange}{zk})(\textcolor{skyblue}{0}+\textcolor{pink}{v_xi}+\textcolor{yellowgreen}{v_yj}+\textcolor{orange}{v_zk})\\
&=\textcolor{skyblue}{wv_xi + wv_yj + wv_zk} + \textcolor{pink}{xiv_xi + xiv_yj + xiv_zk} + \textcolor{yellowgreen}{yjv_xi + yjv_yj + yjv_zk} + \textcolor{orange}{zkv_xi + zkv_yj + zkv_zk} \\
&=\textcolor{skyblue}{w(v_xi+v_yj+v_zk)} + \textcolor{pink}{(-xv_x) + (xv_yk) + (-xv_zj)} + \textcolor{yellowgreen}{(-yv_xk) + (-yv_y) + (yv_zi)} + \textcolor{orange}{(zv_xj) + (-zv_yi) + (-zv_z)} \\
&= \textcolor{skyblue}{w(v_xi + v_yj + v_zk)} + \textcolor{pink}{x(-v_x + v_yk - v_zj)} + \textcolor{yellowgreen}{y(-v_xk - v_y - v_zi)} + \textcolor{orange}{z(v_xj - v_yi - v_z)} \\
&= \textcolor{skyblue}{(wv_xi+wv_yj+wv_zk)}+\textcolor{pink}{(-xv_x+xv_yk-xv_zj)}+\textcolor{yellowgreen}{(-yv_xk-yv_y+yv_zi)}+\textcolor{orange}{(zv_xj-zv_yi-zb_z)}\\
&= \textcolor{skyblue}{(-xv_x-yv_y-zv_z)}+(wv_x+yv_z-zv_y)i+(wv_y+zv_x-xv_z)j+(wv_z+xv_y-y_vx)k
\end{align}
$$
この計算で、元のベクトルに回転の情報が加わりました。
しかし、式の最後の形を見て分かるとおり、w成分が増えてしまっています。(式の青色の成分)
最終的に目指す形はw成分に値が入っていない純クォータニオンなので、このw成分が邪魔ですよね。
ここでさらにかけるのが、共役クォータニオンです。
2_2. 共役クォータニオンをさらにかける
次に、先程の計算結果に共役クォータニオンをかけます。
$$\begin{align}
q v \cdot \overline{q}
\end{align}
$$
$$\begin{align}
&\overline{q} = w - v_xi - v_yj - v_zk
\end{align}
$$
この計算によって、w成分が打ち消しあい、w成分がない純クォータニオンの形になります。
式だけを見ていると、なぜ単位クォータニオンをかけた後に共役クォータニオンをかけるのだろう?と思ってしまいますよね。
途中式を辿ることで、綺麗にw成分が消えるので、「不要なw成分を打ち消しあうためにかけるんだ!」と理解できます!
とても長いですが、頑張ってついてきてください!
なおこれ以降の式では、それぞれの成分を次のように色分けして表示します。
・$\textcolor{skyblue}{w}$成分→$\textcolor{skyblue}{青}$
・$\textcolor{Tomato}{i}$成分→$\textcolor{Tomato}{トマト}$
・$\textcolor{SeaGreen}{j}$成分→$\textcolor{SeaGreen}{深緑}$
・$\textcolor{gold}{k}$成分→$\textcolor{gold}{ゴールド}$
まず、
$$\begin{align}
q \cdot \overline{v} &= \textcolor{skyblue}{(-xv_x-yv_y-zv_z)}+\textcolor{Tomato}{(wv_x+yv_z-zv_y)i}+(\textcolor{SeaGreen}{wv_y+zv_x-xv_z)j}+\textcolor{gold}{(wv_z+xv_y-y_vx)k} \\
&= \textcolor{skyblue}{s} + \textcolor{Tomato}{ai} + \textcolor{SeaGreen}{bj} + \textcolor{gold}{ck}
\end{align}
$$
と置き換えます。
ここで置き換える理由は、そのまま計算すると式がとんでもなく長くなるからです!
このとき、
$$\begin{align}
s &= -xv_x-yv_y-zv_z \\
a &= wv_x+yv_z-zv_y \\
b &= wv_y+zv_x-xv_z \\
c &= wv_z+xv_y-y_vx
\end{align}
$$
です。
これをふまえて、置き換えた式で計算していきます。
$$\begin{align}
q \cdot v \times \overline{q} &=(\textcolor{skyblue}{s}\textcolor{Tomato}{+ai}\textcolor{SeaGreen}{+bj}\textcolor{gold}{+ck})(w\textcolor{Tomato}{-xi}\textcolor{SeaGreen}{-yj}\textcolor{gold}{-zk}) \\
\end{align}
$$
まずはスカラー部分について
$$s(w-xi-yj-zk) = \textcolor{skyblue}{sw}\textcolor{Tomato}{-sxi}\textcolor{SeaGreen}{-syj}\textcolor{gold}{-szk}
$$
ベクトル部分の
・$ai$ 部分について、
$$\begin{align}
ai(w-xi-yj-zk)\\
aiw &= \textcolor{Tomato}{awi} \\
ai(-xi) &= -axi^2 = \textcolor{skyblue}{ax} \\
ai(-yj) &= -ayij = \textcolor{gold}{-ayk} \\
ai(-zk) &= -azik = \textcolor{seagreen}{azj} \\
\end{align}
$$
よって、
$$\textcolor{Tomato}{awi}\textcolor{skyblue}{+ax}\textcolor{gold}{-ayk}\textcolor{seagreen}{+azj}
$$
・$bj$ 部分について、
$$\begin{align}
bj(w-xi-yj-zk) \\
bjw &= \textcolor{seagreen}{bwj} \\
bj(-xi) &= -bxji = \textcolor{gold}{bxk} \\
bj(-yi) &= -byj^2 = \textcolor{skyblue}{by} \\
bj(-zk) &= -bzjk = \textcolor{Tomato}{-bzi} \\
\end{align}
$$
よって、
$$\textcolor{seagreen}{bwj}\textcolor{gold}{+bxk}\textcolor{skyblue}{+by}\textcolor{Tomato}{-bzi}
$$
・$ck$ 部分について
$$\begin{align}
ck(w-xi-yj-zk) \\
ckw &= \textcolor{gold}{cwk} \\
ck(-xi) &= -cxki = \textcolor{seagreen}{-cxj} \\
ck(-yj) &= -cykj = \textcolor{Tomato}{cyi} \\
ck(-zk) &= -czk^2 = \textcolor{skyblue}{cz} \\
\end{align}
$$
よって、
$$\textcolor{gold}{cwk}\textcolor{seagreen}{+cxj}\textcolor{Tomato}{-cyi}\textcolor{skyblue}{+cz}
$$
ここまでをすべてまとめると、
$$\begin{align}
&(\textcolor{skyblue}{sw}\textcolor{Tomato}{-sxi}\textcolor{SeaGreen}{-syj}\textcolor{gold}{-szk})+
(\textcolor{Tomato}{awi}\textcolor{skyblue}{+ax}\textcolor{gold}{-ayk}\textcolor{seagreen}{+azj})+\\
&(\textcolor{seagreen}{bwj}\textcolor{gold}{+bxk}\textcolor{skyblue}{+by}\textcolor{Tomato}{-bzi})+
(\textcolor{gold}{cwk}\textcolor{seagreen}{+cxj}\textcolor{Tomato}{-cyi}\textcolor{skyblue}{+cz})
\end{align}
$$
成分ごとにわけると、
w成分:$\textcolor{skyblue}{sw+ax+by+cz}$
$i$: $\textcolor{Tomato}{-sx+aw-bz+cy}$
$j$: $\textcolor{seagreen}{-sy+az+bw-cx}$
$k$: $\textcolor{gold}{-sz-ay+bx+cw}$
ここからは各成分ごとに、置き換えた $s, a, b, c$ を戻していきます。
※色分けは省略します
[$w$成分]
$sw+ax+by+cz$
・$sw$
$$\begin{align}
sw &= (-xv_x-yv_y-zv_z)\cdot w \\
&= -wxv_x-wyv_y-wzv_z
\end{align}
$$
・$ax$
$$\begin{align}
ax &= (wv_x+yv_z-zv_y) \cdot x \\
&= wxv_x+xyv_z-xzv_y
\end{align}
$$
・$by$
$$\begin{align}
by &= (wv_y+zv_x-xv_z) \cdot y \\
&= wyv_y + zyv_x - xyv_z
\end{align}
$$
・$cz$
$$\begin{align}
cz &= (wv_z+xv_y-yv_x) \cdot z \\
&= wzv_z + xzv_y - yzv_x
\end{align}
$$
全て足し合わせると、
$$\begin{align}
sw+ax+by+cz &= (-wxv_x-wyv_y-wzv_z)+(wxv_x+xyv_z-xzv_y)+(wyv_y + zyv_x - xyv_z)+(wzv_z + xzv_y - yzv_x) \\
&= (-wxv_x+wxv_x)+(-wyv_y+wyv_y)+(-wzv_z+wzv_z)+(xyv_z-xyv_z)+(-xzv_y+xzv_y)+(yzv_x-yzv_x) \\
&= 0
\end{align}
$$
このように、全て打ち消しあって0になります!
これが、単位クォータニオンをかけた後に共役クォータニオンをかけた理由です!
スカラー部が0になるので、この時点で純クォータニオンになりそうなのが分かると思います。
[$i$成分]
$-sx+aw-bz+cy$
・$-sx$
$$\begin{align}
-sx &= -(-xv_x-yv_y-zv_z)\cdot x \\
&= (xv_x+yv_y+zv_z)\cdot x \\
&= x^2v_x+zyv_y+xzv_z
\end{align}
$$
・$aw$
$$\begin{align}
aw &= (wv_x+yv_z-zv_y)\cdot w \\
&= w^2v_x+wyv_z-wzv_y
\end{align}
$$
・$-bz$
$$\begin{align}
-bz &= -(wv_y+zv_x-xv_z)\cdot z \\
&= -wzv_y-z^2v_x+xzv_z
\end{align}
$$
・$cy$
$$\begin{align}
cy &= (wv_z+xv_y-yv_x) \cdot y \\
&= wyv_z+xyv_y-y^2v_x
\end{align}
$$
よって、各ベクトル($vx, vy, vz$)でまとめると、
$$\begin{align}
vx:& \quad (x^2-z^2+w^2-y^2)v_x \\
&= (w^2+x^2-y^2-z^2)v_x
\end{align}
$$
$$\begin{align}
vy:& \quad xyv_y-wzv_y-wzv_y+xyv_y\\
&= (xy-wz-wz+xy)v_y \\
&= (2xy-2wz)v_y
\end{align}
$$
$$\begin{align}
vz:& \quad xzv_z+xzv_z+wyv_z+wyv_z \\
&= 2xzv_z+2wyv_z \\
&= (2xz+2wy)v_z
\end{align}
$$
[$j$成分]
$-sy+az+bw-cx$
・$-sy$
$$\begin{align}
-sy &= -(-xv_x-yv_y-zv_z)\cdot y \\
&= xyv_x+y^2v_y+yzv_z
\end{align}
$$
・$az$
$$\begin{align}
az &= (wv_x+yv_z-zv_y) \cdot z \\
&= wzv_x+yzv_z-z^2v_y
\end{align}
$$
・$bw$
$$\begin{align}
bw &= (wv_y+zv_x-xv_z)\cdot w \\
&= w^2v_y+wzv_x-wxv_z
\end{align}
$$
・$-cx$
$$\begin{align}
-cx &= -(wv_z+xv_y-yv_x)\cdot x\\
&= -wxv_z-x^2v_y+xyv_x
\end{align}
$$
よって、各ベクトル($vx, vy, vz$)でまとめると、
$$\begin{align}
vx: & \quad v_yv_x+wzv_x+wzv_x+xyv_x \\
&= 2wzv_x + 2xyv_x \\
&= (2xy+2wz)v_x
\end{align}
$$$$\begin{align}
vy: & \quad y^2v_y+w^2v_y-z^2v_y-z^2v_y \\
&= (-x^2+y^2-z^2+w^2)v_y \\
&= (w^2-x^2+y^2-z^2)v_y
\end{align}
$$$$\begin{align}
vz: & \quad yzv_z-wxv_z+yzv_z-wxv_z \\
&= 2yzv_z-2wxv_z \\
&= (2yz-2wx)v_z
\end{align}
$$
[$k$成分]
$-sz-ay+bx+cw$
・$-sz$
$$\begin{align}
-sz &= -(-xv_x-yv_y-zv_z)\cdot z \\
&= xv_zz+yzv_y+z^2v_z
\end{align}
$$
・$-ay$
$$\begin{align}
-ay &= -(wv_x+yv_z-zv_y) \cdot y \\
&= -wyv_x-y^2v_z+yzv_y
\end{align}
$$
・$bx$
$$\begin{align}
bx &= (wv_y+zv_x-xv_z) \cdot x \\
&= wxv_y+xzv_x-x^2v_z
\end{align}
$$
・$cw$
$$\begin{align}
cw &= (wv_z+xv_y-yv_x) \cdot w \\
&= w^2v_z+wxv_y-wyv_x
\end{align}
$$
よって、各ベクトル($vx, vy, vz$)でまとめると、
$$\begin{align}
vx: & \quad xv_xz + xzv_x - wyv_x-wyv_x \\
&= 2xzv_x - 2wyv_x \\
&= (2xz-2wy)v_x
\end{align}
$$
$$\begin{align}
vy: & \quad yzv_y+wxv_y+yzv_y+wxv_y \\
&= 2yzv_y + 2wxv_y \\
&= (2yz+2wx)v_y
\end{align}
$$
$$\begin{align}
vz: & \quad z^2v_z-x^2v_z-y^2v_z+w^2v_z \\
&= (-x^2-y^2+z^2+w^2)v_z \\
&= (w^2-x^2-y^2+z^2)v_z
\end{align}
$$
そして、ここまで計算した $v_x, v_y, v_z$ をそれぞれ行列の形で表示してみると次のようになります。
$$R=
\begin{pmatrix}
w^2+x^2-y^2-z^2 & 2xy-2wz & 2xz+2wy \\
2xy+2wz & w^2-x^2+y^2-z^2 & 2yz-2wx \\
2xz-2wy & 2yz+2wx & w^2-x^2-y^2+z^2
\end{pmatrix}
\begin{pmatrix}
vx\\
vy\\
vz
\end{pmatrix}
$$
これで、ベクトルの状態からクォータニオン→回転行列へと変換することができました。
ですが、まだ終わりではないです!
2_3. 単位クォータニオンの性質を利用する
さて、ここで思い出してほしいのは、単位クォータニオンを使って回転を表現していたということです。
前回、クォータニオンの長さは
$$|q| = \sqrt{w^2+x^2+y^2+z^2}
$$
このように表せると書きました。
単位クォータニオンの場合、長さが1になるので式に当てはめると次のようになります。
$$\sqrt{w^2+x^2+y^2+z^2} = 1
$$
ここで両辺を2乗してルートを消します。
すると、次の式が導けます。
$$w^2+x^2+y^2+z^2 = 1
$$
そして、先程導いた回転行列 $R$ は、この単位クォータニオンを使って求めたものでした。
つまり、 $R$ の中に出てくる $w^2+x^2$ などの項は、この「長さ1」の性質を使ってさらに整理することができます。
・1行1列目の成分
$$w^2+x^2-y^2-z^2
$$
単位行列の長さの式から、1行1列目の成分の式にするにはどうすれば良いか考えます。
$w^2+x^2$は同じだから放置して、残った部分について
(単位行列の式) - (?) = (1行1列目の成分)
と考えると、
$$\begin{align}
y^2 - 2y^2 = -y^2 \\
z^2 - 2z^2 = -z^2 \\
\end{align}
$$
となるので、$-2y^2-2z^2$ 単位行列の式に足せば良さそうです。
よって、
$$\begin{align}
w^2+x^2-y^2-z^2 &= (w^2+x^2+y^2+z^2) - 2y^2-2z^2 \\
&= 1- 2y^2-2z^2 \\
&= 1-2(y^2+z^2)
\end{align}
$$
これで、1行1列目の成分がさらに短く書き換えられました!
同様に2行2列目、3行3列目でもおこないます。
・2行2列目の成分
$$w^2-x^2+y^2-z^2
$$
これを単位行列の長さの式から、2行2列目の成分の式にするにはどうすれば良いか考えると、
$w^2+y^2$は同じだから放置して、残った部分について
(単位行列の式) - (?) = (2行2列目の成分)
と考えると、
$$\begin{align}
x^2 - 2x^2 = -x^2 \\
z^2 - 2z^2 = -z^2
\end{align}
$$
となるので、$-2x^2-2z^2$ 単位行列の式に足せば良さそうです。
よって、
$$\begin{align}
w^2-x^2+y^2-z^2 &= (w^2+x^2+y^2+z^2) - 2x^2-2z^2 \\
&= 1-2x^2-2z^2 \\
&= 1-2(x^2+z^2)
\end{align}
$$
・3行3列目の成分
$$w^2-x^2-y^2+z^2
$$
これを単位行列の長さの式から、3行3列目の成分の式にするにはどうすれば良いか考えると、
$w^2+z^2$は同じだから放置して、残った部分について
(単位行列の式) - (?) = (3行3列目の成分)
と考えると、
$$\begin{align}
x^2 - 2x^2 = -x^2 \\
y^2 - 2y^2 = -y^2
\end{align}
$$
となるので、$-2x^2-2y^2$ 単位行列の式に足せば良さそうです。
よって、
$$\begin{align}
w^2-x^2-y^2+z^2 &= (w^2+x^2+y^2+z^2) - 2x^2-2y^2 \\
&= 1-2x^2-2y^2 \\
&= 1-2(x^2+y^2)
\end{align}
$$
これで3つの成分を書き換えられました!
最後に全てまとめると、クォータニオン→回転行列へ変換すると次のようになります。
$$R=
\begin{pmatrix}
1-2(y^2+z^2) & 2xy-2wz & 2xz+2wy \\
2xy+2wz & 1-2(x^2+z^2) & 2yz-2wx \\
2xz-2wy & 2yz+2wx & 1-2(x^2+y^2)
\end{pmatrix}
\begin{pmatrix}
vx\\
vy\\
vz
\end{pmatrix}
$$
おわりに
クォータニオンから回転行列への変換を導出できました!
次回の後編では、今回の操作の「逆」を行って、回転行列からクォータニオンの変換について解説していきます。
次の記事はこちらから
参考リンク
この記事を作るにあたり、以下のサイトを参考にしました。
・CGのための数学(Zenn)
・クォータニオンと回転行列 - 理系的な戯れ
 ことれいのもり
ことれいのもり








