回転行列とクォータニオンを、数学初心者でも理解できるように丁寧に解説する【前編：基礎知識】

2025-06-09

はじめに

ゲーム制作をしていると、一度は耳にする「クォータニオン」という言葉。

今までライブラリに任せて使ってきましたが、「回転行列→クォータニオン」の変換を自前で実装しなければならない場面に出くわしました。

ですが、ここで大きな問題が立ち塞がります。

クォータニオンの説明記事が数式だらけすぎて理解できない！！

数学が得意な人向けの記事ばかりで、私のように「数学はちょっと苦手だけど、仕組みを理解して実装したい」という人にはハードルが高い物ばかり。

そこで前編のこの記事では、「回転行列 → クォータニオン」の変換を実装するために必要なクォータニオンの基礎知識だけに絞って、なるべくかみ砕いて説明していきます。

内容に間違いがあるかもしれないので、「参考のひとつ」として読んでもらえるとありがたいです。

本記事について（3部構成）

この記事は「回転行列→クォータニオン変換の式を自力で導出する」ことを最終目標とした、3部構成の前編（基礎知識編）です。

前編（この記事）：クォータニオン、回転行列とtraceの知識を解説
中編：[クォータニオンから回転行列への変換を、数式と手計算で丁寧に導く【中編】]（https://kotorei.com/gamemath/quaternion-to-rotation-matrix-beginner）
後編：[回転行列からクォータニオンの変換式を4パターンに分けて丁寧に導出する【後編・本題】]（https://kotorei.com/gamemath/rotation-matrix-to-quaternion-4-patterns）

「導出なんて難しそう」と思うかも知れませんが、基礎知識さえ理解すれば、誰でもたどり着けるように工夫しています。

途中式を省略することなく丁寧に解説しているので、興味のあるところから読み進めてみてください。

本記事で説明すること

回転行列→クォータニオンの変換を実装するために知っておくべき知識は以下の5つです。

クォータニオンとはどんな形で表されるのか
純クォータニオン
単位クォータニオン
共役クォータニオン
回転行列とトレース（trace）の関係

またこの記事では、複素数と比べる形でクォータニオンの説明をしていきます。

クォータニオンなのになんで複素数？と思うかもしれません。

その理由は、クォータニオンは複素数を拡張したものだからです。

ひとつずつ丁寧に説明していきますので、複素数の知識が無くても大丈夫です！

クォータニオンの表し方

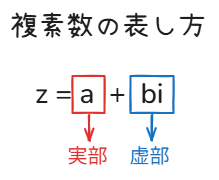
複素数の表し方

複素数は一般的にこのように書き表せます。

$$z = a + bi $$

このとき、aを実部といい、biを虚部と言います。

実部 + 虚部　という組み合わせです。

図で表すとこんな感じ。

複素数の表し方

クォータニオンの表し方

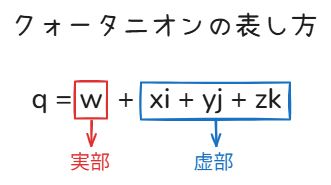
ではクォータニオンはどのように書き表せるでしょうか。

複素数では実部 + 虚部でしたが、クォータニオンは虚部が2つ増えてこんな形になります。

$$q = w + xi + yj + zk $$

図で表すとこんな感じ。

クォータニオンの表し方（実部と虚部）

ここで、虚部にある i, j, k　は、虚数の性質を持っています。

つまり、2乗すると-1になります。

$$i^2 = j^2 = k^2 = -1 $$

さらにこれだけでなく、以下のような性質があります。

$$\begin{gathered} ijk = -1 \\ ij = -ji = k \qquad jk = -kj = i \qquad ki = -ik = j \end{gathered} $$

なんだか難しそう・・・！

でも、「i, j, kの間でいろいろ変換できるんだな」ぐらいの認識で大丈夫です。

ところで先程のクォータニオンの式について、特に虚部の係数をよく見ると何かに気がつきませんか？

x, y, z に虚数単位が掛け算してありますよね。

x, y, zと言えば、ベクトルです！！

つまり、こう言えます。

$$\vec{v} =(x, y, z) $$

このように置くと、

$$q = (w, \vec{v}) $$

という風に、さらに短縮して書けます。

このとき、wの部分をスカラー部、vの部分をベクトル部と言います。

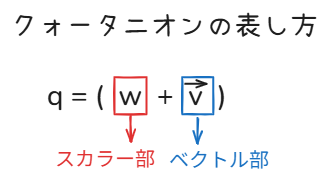
クォータニオンの表し方（スカラー部とベクトル部）

これが基本的なクォータニオンの形です。

ここからさらに、特別な名前がついているものを紹介します。

純クォータニオン

クォータニオンの中でも、スカラー部のwが0のものを純クォータニオンと呼びます。

$$q = 0 + xi + yj + zk $$

単位クォータニオン

長さが1のクォータニオンを単位クォータニオンと呼びます。

実際に計算で導いてみましょう。

複素数の絶対値

まずは複素数の絶対値から考えてみます。

絶対値とは原点からの距離を表すもので、複素数 $a + bi$ の絶対値は、次のように求めることができます。

$$|z| = \sqrt{a^2+b^2} $$

クォータニオンの絶対値と正規化

クォータニオンも同様に、次の式で絶対値（長さ）を求めることができます。

$$|q| = \sqrt{w^2+x^2+y^2+z^2} $$

このように絶対値が定義できるということは、クォータニオンも正規化（normalize）できます。

正規化とは、向きを変えずに長さを1に揃える操作のことです。

クォータニオンを正規化するには、自身をその絶対値で割ります。

つまり、クォータニオン($q = w + xi + yj + zk$)を正規化すると、

$$normalize(q) = \frac{w}{|q|} + \frac{x}{|q|}i + \frac{y}{|q|}j + \frac{z}{|q|}k $$

となります。

こうして得られた長さが1のクォータニオンが単位クォータニオンです。

注意

今後出てくる計算では、単位クォータニオンを $q=w+xi+yj+zk$ の形で使います。

これは、正規化した後の結果をこのように表しているだけです。

つまり、正規化する過程で各成分($w, x, y, z$)をその絶対値で割った結果、最終的にこのように表しているだけです。

単位クォータニオンの説明でさっきは分数の形だったのに、なんでいきなり$q=w+xi+yj+zk$になったの？と思うかもしれません。

そうではなく、正規化した後の結果をただ単に $q=w+xi+yj+zk$ と表しているだけなんだよ！ ということを覚えておいてください！！

共役クォータニオン

共役複素数

複素数 $a+bi$ に対して、 $a-bi$ を共役複素数 と言います。

簡単に言うと、虚部の符号を反転したものです。

共役クォータニオン

クォータニオンも同様に共役が存在します。

複素数と同じく、虚部の符号をマイナスにしたものです。

つまり、 $q = w + xi + yj + zk$　ならば、

$$\overline{q} = w - xi - yj - zk $$

と表せます。

これらの4つが今回抑えておくべきクォータニオンについての知識です。

回転行列とトレース（trace）の関係

最終的にやりたいことは、回転行列→クォータニオンへの変換です。

そのため、回転行列について少し知っておきましょう。

n軸周りの回転行列

本来ゲーム制作で使う行列は4x4が多いですが、今回はわかりやすさ重視のために3x3で考えていきます。

まず、3x3の行列Rがあるとします。

$$R = \begin{pmatrix} r_{00} & r_{01} & r_{02} \\ r_{10} & r_{11} & r_{12} \\ r_{20} & r_{21} & r_{22} \\ \end{pmatrix} $$

このときのx軸周り・y軸周り・z軸周りの回転行列は以下のように表されます。

x軸周り

$$R_x(θ) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & cosθ & -sinθ \\ 0 & sinθ & cosθ \\ \end{pmatrix} $$

y軸周り

$$R_y(θ) = \begin{pmatrix} cosθ & 0 & sinθ \\ 0 & 1 & 0 \\ -sinθ & 0 & cosθ \\ \end{pmatrix} $$

z軸周り

$$R_z(θ) = \begin{pmatrix} cosθ & -sinθ & 0 \\ sinθ & cosθ & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$

トレース（trace）

行列において、対角成分の和を行列の トレース(trace) と言います。

先程の回転行列Rで考えると、斜めになっている部分、つまり

$$r_{00}, r_{11}, r_{22} $$

の和のことです。

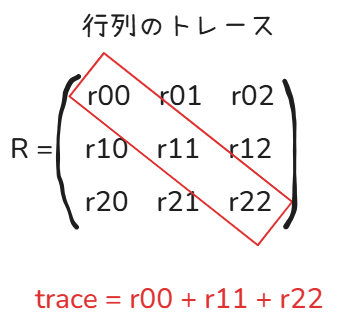
行列のトレース

まずは、回転していないときの行列 = 単位行列のときのtraceを見てみましょう。

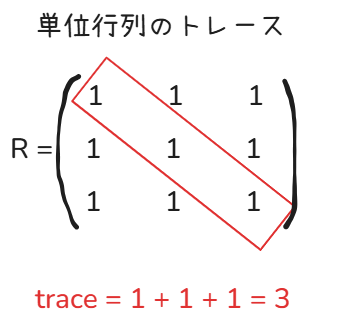
単位行列のトレース

斜めになっている成分は全て1なので、これを足し算します。

つまり、回転していないときのtraceの値は3です。

回転しているときのトレース（trace）

では、回転しているときのtraceの値はどうなるでしょうか。

z軸周りに90度回転する行列
z軸周りに180度回転する行列

この2パターンを見ていきましょう。

z軸周りに90度回転する行列

$$\begin{align} R_z(90) &= \begin{pmatrix} cos90 & -sin90 & 0 \\ sin90 & cos90 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \\ &= \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \end{align} $$

よって、z軸周りに90度回転したときのトレースは、

$$trace = 0 + 0 + 1 = 1 $$

z軸周りに180度回転する行列

$$\begin{align} R_z(180) &= \begin{pmatrix} cos180 & -sin180 & 0 \\ sin180 & cos180 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \\ &= \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \end{align} $$

よって、z軸周りに180度回転したときのトレースは、

$$trace = -1 + -1 + 1 = -1 $$

ここまでの結果をまとめると、

単位行列（回転していない）： $trace = 3$

z軸周りに90度： $trace = 1$

z軸周りに180度： $trace = -1$

traceの値が3に近いほど回転していない と言えます。

つまり、traceの値によってこの行列が回転しているかがざっくり分かることになりますね！

w成分とtraceの関係

さらに回転行列のtraceから、クォータニオンのw成分を求める公式があります。

$$\begin{align} w &= \frac{1}{2}\sqrt{1+r_{00}+r_{11}+r_{22}} \\ &= \frac{1}{2}\sqrt{1+trace} \\ \end{align} $$

この方法を使って、先程と同様に単位行列（回転なし）・z軸周りに90度・z軸周りに180度の場合を計算してみましょう。

単位行列（回転なし）

$$\begin{aligned} \text{trace} &= 3 \\ w &= \frac{1}{2}\sqrt{1+3} \\ &= \frac{1}{2}\sqrt{4} \\ &= \frac{1}{2} \cdot 2 \\ &= 1 \end{aligned} $$

よって、単位行列のときは $trace = 3, w = 1$ と分かりました。

z軸周りに90度回転

$$\begin{aligned} \text{trace} &= 1 \\ w &= \frac{1}{2}\sqrt{1+1} \\ &= \frac{1}{2}\sqrt{2} \\ &= \frac{1}{2} \cdot 1.414... \\ &\risingdotseq 0.70... \end{aligned} $$

よって、z軸周りに90度回転しているときは $trace = 1, w \risingdotseq 0.70$ と分かりました。