視錐台のNear/Far面の高さにtanを使って計算する理由を分かりやすく解説

はじめに

OpenSiv3Dなどの3Dエンジンで視錐台を描画するとき、以下のようなコードがあります。

double nearHeight = 2.0 * Math::Tan(fovDegree / 2.0) * nearClip;

この数式は、視錐台のNear面やFar面の「高さ」を計算するために使われます。

しかし、この式の意味をしっかり理解している人は、意外と少ないかもしれません。

この記事では、「なぜtanが使われるのか？」「どの三角形を表しているのか？」を図を使って丁寧に解説します。

Near面・Far面とは？

まずは、Near面・Far面がどこにあるかを確認しましょう。

Near面とは、カメラの見え始める距離のことです。

一方、Far面とは見えなくなる限界の距離のことです。

Near面～Far面の間にあるものをカメラは描画します。

図で見てみましょう。

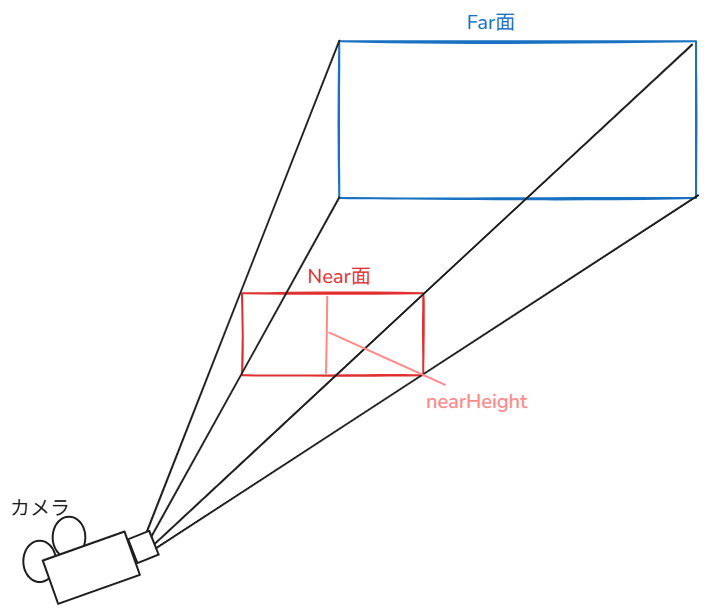
手前の赤い面がNear面、青い面がFar面です。

このうち、Near面の高さが今回求めたい「nearHeight」です。

1. 直角三角形を作る

nearHeightを求めるにはどうしたらいいでしょうか？

注目すべきは、直角三角形を作ることです。

カメラの位置、nearHeightの高さの半分（nearHeight/2）、カメラの位置からnear面までの距離（nearClip）で直角三角形が作れます。

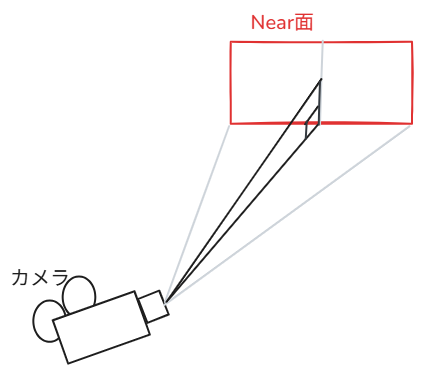
図でいうと、黒い三角形の部分です。

ここで直角三角形ができます。

2. tanの式を作る

この三角形を横からみて考えてみましょう。

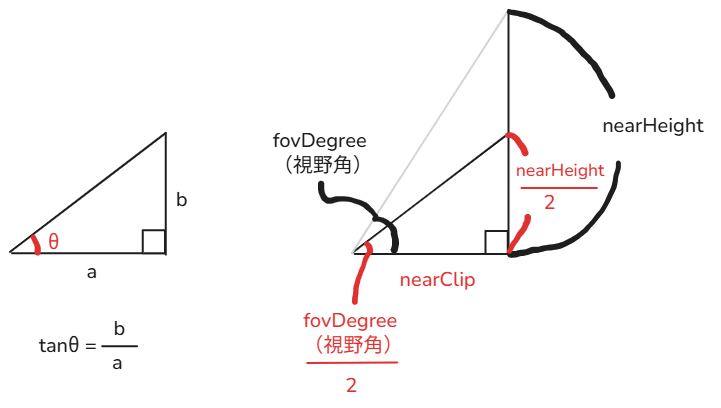
tanの公式は、

$$ tanθ = \frac{b}{a} $$

で表せます。

同じ式をNear面で作ると、こうなります。

$$ tan(\frac{fovDegree}{2}) = \frac{\frac{nearHeight}{2}}{nearClip} $$

fovDegreeは視野角のことです。

θはちょうど視野角の半分になります。

これをnearHeightについて解いていきます。

$$ \begin{align} tan(\frac{fovDegree}{2}) &= \frac{\frac{nearHeight}{2}}{nearClip} \\ &= \frac{nearHeight}{2 * nearClip} \\ nearHeight &= tan(\frac{fovDegree}{2})*2*nearClip \end{align} $$

この式は、一番最初のコードの式と一致します。

double nearHeight = 2.0 * Math::Tan(fovDegree / 2.0) * nearClip;

これで、nearHeightの式が求まりました！

FarHeightも全く同じ手順で求めることができます。

    // Near・Far面の高さを計算する
    double nearHeight = 2.0 * Math::Tan(fovDegree / 2.0) * nearClip;
    double farHeight = 2.0 * Math::Tan(fovDegree / 2.0) * farClip;

おわりに

今回の記事では、視錐台のNear面やFar面の高さを求める式に、tanを使うのかを図と一緒に解説しました。

直角三角形をみつけることで、シンプルに導けることが分かったと思います。

なんとなく使っていた式の意味が少しでも明確になれば幸いです。