ことれいのもり
はじめに
DirectX11からHLSLのシェーダーへ行列を送るとき、わざわざ転置行列にして送る理由が気になったので調べてみました。
私は元々数学に強くなく、行列も聞いたことある程度で詳しい部分までは知りません。
インターネットの海をさまよっても数学に詳しい前提の記事が多くて心が折れそうになりました。
そのような数学詳しくない人向けに頑張って説明してみます。
自分でも分かるレベルにまでかみ砕いたので難しい数式はないはずです！
DirectXでシェーダーへ行列を送る時に転置する理由を詳しく解説
2025-07-31
前提
言語
- C++
- DirectX11
- HLSL
疑問に思った部分
今回疑問に思ったのは、DirectX11でHLSLへ行列を渡すときです。
その部分が下のコードです。
void Renderer::Render()
{
// ビュー・プロジェクション行列
DirectX::XMMATRIX viewMatrix = camera->GetViewMatrix();
DirectX::XMMATRIX projectionMatrix = camera->GetProjectionMatrix();
DirectX::XMMATRIX viewProjectionMatrix = DirectX::XMMatrixMultiply(viewMatrix, projectionMatrix);
// 行列を転置して、
// 定数バッファを作成
MatrixBufferType matrixData;
matrixData.world = DirectX::XMMatrixTranspose(DirectX::XMMatrixIdentity());
matrixData.viewProjection = DirectX::XMMatrixTranspose(viewProjectionMatrix);
// ...
// 省略
// ...このコードはHLSLに行列を送ろうとしている処理です。
そのままデータを送るのではなく、転置行列を使った上で送らないとうまくいきません。
これがなぜなのかを調べました。
大きく分けると二つの疑問です。
１． そもそもなぜ転置をする必要があるのか？
２． なぜ転置をするとうまくいくのか？
この二つについて説明します。
行優先と列優先
まず、行列には行優先と列優先の2種類があります。
4x4の行列を考えてみましょう。
これはメモリ空間上をイメージした図です。
左の番号がメモリで、0番目はメモリ0番目をイメージしています。
a11は1行1列目を意味します。
行優先は行の方向（横方向）に順番に値を入れていきます。
配列を格納するイメージに近いですね。
DirectXやC++がこの方法を使っています。
一方列優先は列の方向（縦方向）に順番に値を入れていきます。
HLSLやGLSLがこの方法を使っています。
行列を格納するとき、この2通りがあることになります！
つまり、C++からHLSLへ行列を渡すときに行列の格納方法が違うことを考慮する必要があるということになります。
いやいや、別にどっちでもよくね？と思いませんか？（私は思いました。）
実は重大な問題があるんです！
それは掛け算の計算をするときです。
行列の掛け算
行列の掛け算を覚えているでしょうか。
覚えていない人はぜひ復習してください。
2つの行列A, Bがあるとします。
Aの1行目 とBの1列目の成分同士をかけた和が左上にきます。
計算式では 1x5+2x7です。よって左上は19。
次にAの1行目とBの2列目の成分同士をかけて和を取ると22, … と計算することができます。
行列のかけ算の性質1：交換法則が成り立たない
行列のかけ算では、交換法則が成り立ちません。
A x Bの計算結果と B x Aの計算結果は異なります。
試しにB x Aを行なってみましょう。
計算結果が異なることが分かりますね。
行列の掛け算では計算順序が異なると結果が変わるという事実を覚えておいてください！行列の掛け算の性質2：行列Aの列数と行列Bの行数が同じ時のみ計算可能
行列のかけ算はそもそも計算できない場合が存在します。
例えば、行列Cが2x2行列、行列Dが3x2行列として計算してみましょう。
計算すると、行列Dの5と6の計算相手が行列Cに存在しません。
これは行列Cの列数が2、行列Dの行数が3となるのでそもそも計算不可です。
よって、行列Cの列数と行列Dの行数が同じ時のみ計算ができます。
この2つの性質をおさえた上で、行優先と列優先の話に戻ります。
行優先・列優先でかけ算をしてみる
行優先のとき
ある座標P（x, y, z, w）に対して、4x4行列Mをかけてビュー行列を作りたいとします。
座標Pは行優先なので横に並んでいると考えて、1x4行列、行列Mは4x4行列です。
さきほどの「性質2：行列Aの列数と行列Bの行数が一致したときのみ計算できる」を思い出してみると、
行優先の時、P x Mしかできません。
つまり、行優先の時は行列Mは右からかけることしかできないのです！
列優先のとき
同じように列優先でも試してみます。
ある座標P（x, y, z, w）に対して、4x4行列Mをかけてビュー行列を作りたいとします。
この座標Pは列優先なので縦に並んでいると考えて、4x1行列、行列Mは4x4行列です。
列優先の時、M x Pしかできません。
つまり、列優先の時は行列Mは左からかけることしかできないのです！
二つを見比べてみると
ここまでの話をまとめると
行優先のとき：P x M
列優先のとき：M x P
つまり、C++やDirectXでは行優先なので P x Mで計算しますが、HLSLでは列優先なので M x Pで計算します。
行列のかけ算の性質で交換法則は成り立たないので、両者の計算結果は異なります。
C++で生成した行列Mは右からかけられると思っていたのに、HLSLでは列優先なので左からかけられてしまい、本来とは違う計算結果になってしまうのです！！！
これが、行優先から列優先に移動するときにそのままデータを渡すだけではダメな理由です。
ではどうやってデータを渡せば問題ないのでしょうか？
転置行列
ここで出てくるのが転置行列です。
転置行列とは 行と列を入れ替えた行列のことです。
これをさきほどの座標Pで考えてみると、
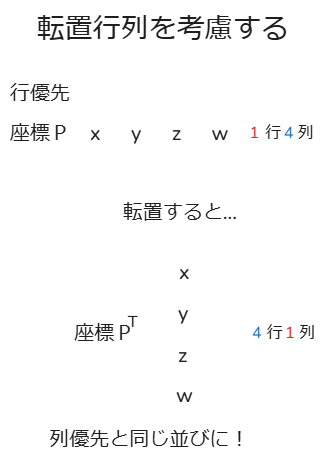
行優先の行列に転置をとると列優先になります！！
これだけだと並びが変わっただけで意味がなさそうですが、転置行列にはある性質があります。
Aを m x n 行列、Bを n x l 行列とすると、
AとBの行列の積を転置したものは、Bの転置 x Aの転置と等しくなります。
同じように座標Pで考えてみると
このように右からかける行列から左からかける行列へ変換できるのです！
まとめ
- そもそもなぜ転置をする必要があるのか？
C++では行優先なので行列を右からかけるが、HLSLでは列優先なので行列を左からかける。
かけ算の順番が変わると行列は結果が異なるのでそのまま送ることはできない。
転置をすると行優先から列優先へ変換できる。
- なぜ転置をするとうまくいくのか？
「行列ABの積を転置したものは、行列Aの転置と行列Bの転置の積と等しい」という性質があり、これにより行列のかける順番が変わると結果が変わるという問題を解決できるから。
おわりに
二つの疑問を軸にして説明したのでかなり分かりやすくなったと思います。
行列の偉大さが分かりますね！
